A Young Person's Guide to the Principles of Music Synthesis
Table of Contents
- Table of Contents
- Introduction
- Sound Waves and Oscillators
- Building a Synthesizer
- Conclusion and Further Reading
Introduction
This article is a (relatively) brief introduction to the principles of music synthesis. Each of the basic components of synthesizers are explained, along with descriptions and examples of how these components are chained together to make interesting sounds. The principles discussed are not unique to any specific synthesis platform, but are applicable to music synthesis in general.
I hope this article will help interested musicians and composers access the academic tools and literature associated with electronic music. Most electronic music literature assumes a linguistic and conceptual vocabulary which is opaque and inaccessible to the beginner. There's no good reason for this. This article is intended as a good place to start learning; a place to acquire vocabulary without technical training.
The text of this article is accompanied by illustrations, audio examples, and links to working demonstrations in PureData. PureData is a powerful, free, cross-platform, open source music synthesis tool. It's a good idea to read this article with PureData open in the background, building and learning as you go.
You can download PureData by clicking here. It's available for Linux, Mac OS X, and Windows. The examples provided with this article were created with and tested on PureData 0.40.1 for Mac OS X.
All of the PureData examples are collected in this zip file.
Sound waves and oscillators
Sounds are pressure waves which travel through air, or another medium, to our ears. Unlike waves in the ocean, which move up and down, pressure waves move forward and back. These waves move our ear drums in and out, and we experience this as sound. Sound synthesis is the art of creating signals that, when turned into sound waves by a speaker, people find interesting. During the course of this article we'll explore a number of devices that create and modify signals used to synthesize sound.
The first such device we'll consider is called an oscillator. An oscillator generates a consistent, repeating signal. Signals from oscillators and other sources are used to control the movement of the cones in our speakers, which make real sound waves which travel to our ears. If you tie one end of a rope to a doorknob, stand back a few feet, and wiggle the other end of the rope up and down really fast, you're doing roughly the same thing as an oscillator. The difference is that you're wiggling a rope, whereas the oscillator is wiggling an audio signal.
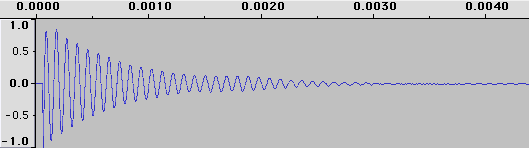
Audio signals are often represented on a graph where the horizontal x-axis represents time and the vertical y-axis represents the pressure of the signal. This is called a time domain representation of audio. Time domain graphs are kind of like instructions for speakers about how to move in and out. When the graph reads 1, the speaker cone is pushed all the way out, when it reads -1, the cone is pulled all the way in. This movement creates a pressure wave in the air which we hear as sound. If a speaker cone moves in and out according to the graph above, it will make the sound of a bass drum.
Frequency and pitch
The rate at which a sound wave moves in and out is called the frequency. Frequency is measured in cycles per second. The length of a singal cycle of a waveform is the span of time it takes for that waveform to repeat. People generally hear an increase in the frequency of a sound wave as an increase in pitch. When the frequency of an oscillator is doubled, the pitch of the sound it generates moves an octave up. For example, an oscillator generating a signal that repeats at the rate of 440 cycles per second will have the same pitch as middle A on a piano. An oscillator generating a signal that repeats at 880 cycles per second will have the same pitch as the A an octave above middle A. A common way of saying "cycles per second" is "Hertz," abbreviated "Hz."
Basic waveforms
There are four different types of basic wave shapes, or waveforms, illustrated here.
Technical note: Topics in music synthesis sometimes call for a little bit of math. If you're not a math person, that's okay, you can skip over the stuff that doesn't make sense. To make it easier for you, the parts you can skip will be safely contained in these sturdy boxes.
Sine
Sine waves look similar to a gentle wave in a bowl of water, moving up and down with no abrupt starts or stops. Common sounds similar to a sine wave include whistling, air blowing across the opening of an empty bottle, and a ringing tuning fork.
Technical note: The sine wave is the most basic, pure waveform, with a contour described by a trigonometric function called the sine function. Any other waveform, including the other simple waveforms described below, can be created by adding up a series of sine waves. Details on this process exceed the scope of this article. For more information, check out the Wikipedia entries on Fourier Analysis and Additive Synthesis.
In the above picture, the first two sine waves are added together to produce a third, different wave.
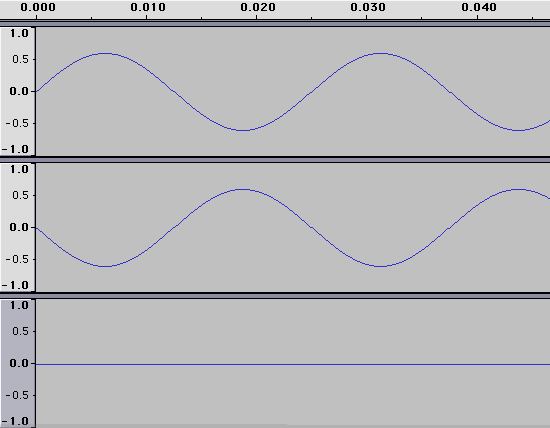
In the above picture, a sine wave is added to its opposite. The result is silence.
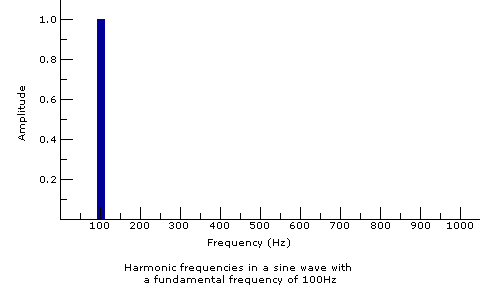
The above chart represents an audio signal based on its frequency. This is called a frequency domain graph. Some stereo systems have an LCD screen where lines rise and fall based on the pitch content of the sounds being played. That LED screen is a frequency domain representation of the audio. As shown in the chart above, a sine wave would only push up one of these lines. This is because sine waves, the simplest waves, have only one frequency. More complicated waves can have energy at more than one frequency, and a graph is a good way to keep track of what's going on. We'll look at frequency domain graphs of more complicated waves very soon.
Sawtooth
Audio example of sawtooth waves.
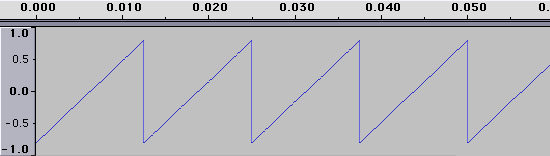
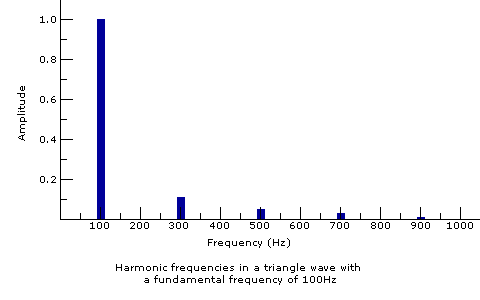
Sawtooth waves, also called saw waves, have a very strong, clear, buzzing sound. A sawtooth wave can be made by adding a series of sine waves at different frequencies and volume levels. The frequency of the first, loudest sine wave is what we hear as the frequency of the resulting sawtooth. This is called the fundamental frequency. Each of the other, progressively quieter, sine waves that make up a sawtooth have frequencies which are integer multiples of the fundamental frequency. These frequencies are called harmonics.
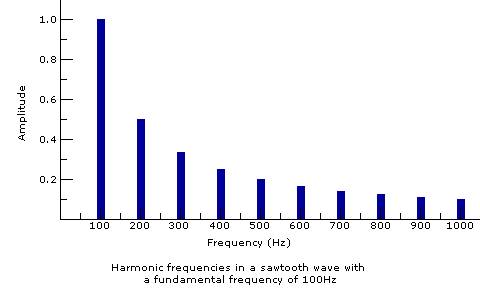
For example, an ideal sawtooth wave with a fundamental frequency of 100Hz would have harmonics at 200Hz, 300Hz, 400Hz, and so on to infinity, with each harmonic quieter than the last. Because the sawtooth wave contains every integer harmonic of the fundamental frequency, it sounds very rich to our ear. The fundamental frequency defines the pitch of the sound, while the harmonics change the character, or timbre, of the sound without affecting the pitch.
Technical note: The amplitude of a given harmonic in a sawtooth wave is equal to the inverse of its harmonic number. For example, a sawtooth wave with a fundamental frequency of 100Hz and an amplitude of 1 would have a harmonic at 200Hz (100*2) with an amplitude of 0.5 (1/2), another harmonic at 300Hz (100*3) with an amplitude of 0.33 (1/3), and so forth. The more harmonics are added in this manner, the more the wave will look like the idealized sawtooth wave depicted in this article.
Square
Audio example of square waves.
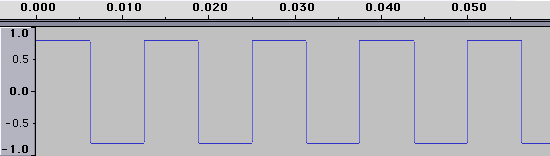
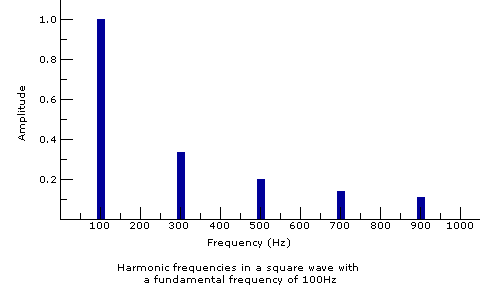
Square waves have a rich sound that's not quite as buzzy as a sawtooth wave, but not as pure as a sine. Old Nintendo game soundtracks were made almost exclusively from square waves. Like sawtooth waves, square waves can be generated by adding a series of sine waves with decreasing volume. However, the square wave contains only the odd numbered harmonics.
The amplitude of a given harmonic in a square wave is equal to the inverse of its harmonic number. For instance, a square wave with a fundamental frequency of 100Hz would have a harmonic at 300Hz (100*3) with an amplitude of 0.33 (1/3).
Triangle
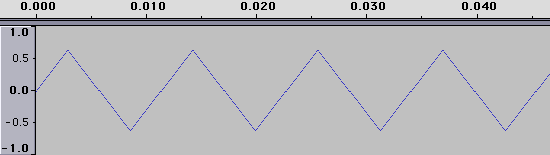
Audio example of triangle waves.
Triangle waves sound like something between a sine wave and a square wave. Like square waves, they contain only the odd harmonics of the fundamental frequency. They differ from square waves because the volume of each added harmonic drops more quickly.
Technical note: The amplitude of a given harmonic in a triangle wave is equal to the inverse square of its harmonic number. For example, a triangle wave with a fundamental frequency of 100Hz and an amplitude of 1 would have a harmonic at 300Hz (100*3) with an amplitude of 0.1111 (1/3^2).
Building a Synthesizer
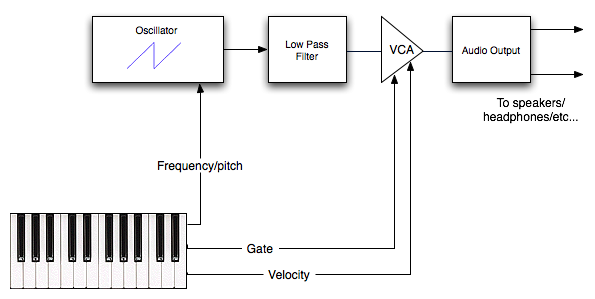
Now that we understand oscillators, let's draw a diagram of a very simple synthesizer. This synthesizer will contain a single sawtooth oscillator which sends signal to our audio output, and then to our speakers. The pitch of the oscillator will be controlled by a keyboard.
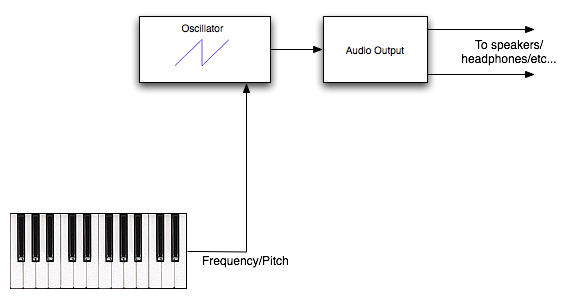
Here's a sample of what the synthesizer described in this diagram might sound like.
Here's a realization of this patch in PureData.
Individual synthesizer components which perform a single, simple function—such as oscillators and filters—are called modules. A modular synthesizer is a synthesizer made by linking together lots of small modules in interesting ways. In the diagrams we use, the lines connecting the modules are like virtual cables, sending signal between them in much the same way an audio cable would in real life.
Volume control
There are some problems with our synthesizer design—not the least of which is that because we have no way of controlling the volume of the oscillator, our instrument is always making sound! In order to fix this problem, we need to add a module called a Voltage Controlled Amplifier, or VCA. The function of a VCA is to raise or lower the volume, often called amplitude or level, of a signal. Essentially, a VCA is a volume knob. Oscillators and other sound generating modules are always making sound, and VCAs are what keep the level down when you're not playing.
In analog synthesizers, VCAs are actually controlled by wires carrying electrical current. There are no real wires carrying voltage inside a virtual synthesizer, but people often call virtual amplitude controls VCAs anyway. With many synthesizers, most of the VCAs are beneath the hood and we don't need to worry too hard about where they are or how they're controlled, but it's important to know how they work.
Let's add a VCA to our simple synthesizer now. This means adding a new module and a couple more cables, but don't worry, they're explained right after the diagram.
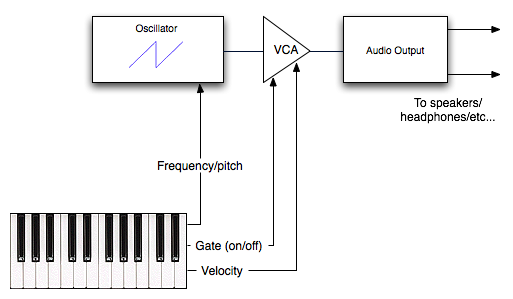
Here's a sample of what the synthesizer described in this diagram might sound like. Note that we can now insert pauses and play notes at different volumes.
Here's a realization of this patch in PureData.
The "gate" cable running from the keyboard to the VCA is a signal that sends one of two messages to the VCA: "on" if a key is depressed, and "off" otherwise. When the gate signal is off, or closed, we hear nothing. When the gate signal is on, or open, then the VCA will let the noise from the oscillator to the audio output. The "velocity" cable sends a level to the VCA that corresponds with how fast we hit the key, and controls the volume level of the output. If we press a key very hard, and thus very fast, the volume of the output will be louder than if we pressed the key soft and slow.
Filters
Filters are, generally speaking, tools for manipulating signals. Any device which modifies a signal in any way is, technically, a filter. When people talk about filters, however, they usually are referring to filters which modify the harmonic content of the signal, altering the characteristics of the sound in the frequency domain. This is the sense in which the term "filter" is used in this article.
Filters allow you to select a range of frequencies in a sound, and either amplify or reduce those frequencies. Decreasing high frequencies or increasing low frequences within a sound makes it seem "darker" or muffled, while increasing high frequencies or decreasing low frequences makes the sound seem "brighter." Filtering like this happens in real life all the time. If you're talking to someone and hold a large book in front of your mouth, the book filters out much of the high frequency content of your voice, causing it to sound dark and muffled.
Low pass and high pass filters
Audio example of a low pass filter.
Audio example of a high pass filter.
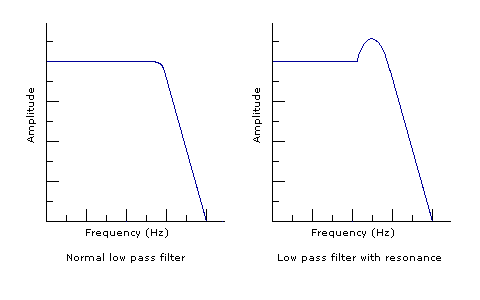
A low pass filter allows low frequencies to pass through the filter and blocks out high frequencies, causing the sound to seem muffled. The range of frequencies blocked by a filter is called the stop band. The range of frequencies allowed to pass through the filter is called the pass band. The transition from pass band to stop band is gradual, and happens over a range called the transition band. The width of the transition band depends on the rate at which the filter reduces the signal. This rate is called the slope, which is measured in decibels per octave. (A detailed discussion of the decibel as a unit of amplitude measurement is beyond the scope of this article. As always, the Wikipedia article on decibels delivers the goods.) The frequency where the filter has reduced the level of the signal to about seven tenths its original level is called the cutoff frequency. A high pass filter does the opposite of a low pass filter: blocks low frequencies and lets high frequencies pass through.
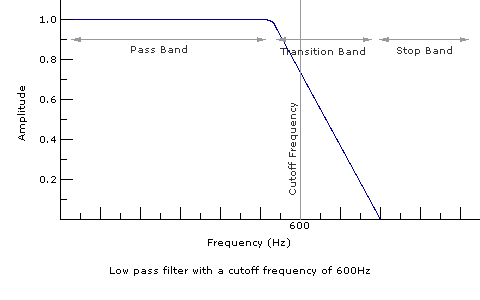
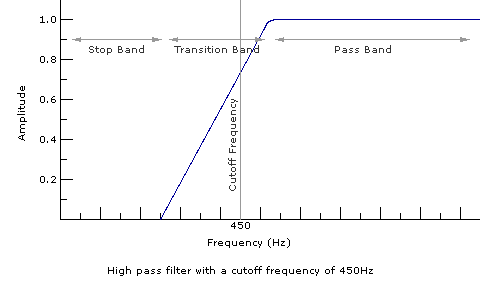
Technical note: The exact amount of level reduction that defines the cutoff frequency of a filter is 0.707 times the maximum level of the signal. The power of a signal is proportional to the amplitude of the signal squared, and at 0.707 times the maximum level, the power has dropped in half. For this reason, the cutoff frequency is also called the "half-power point." Since this drop in power results in a drop in volume of about 3 decibels, the cutoff frequency can also be called the "3dB point."
Band pass and band reject filters
Audio example of a band pass filter.
Audio example of a band reject filter.
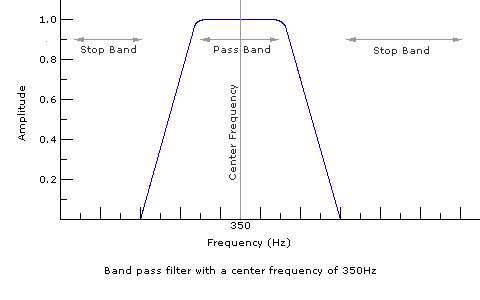
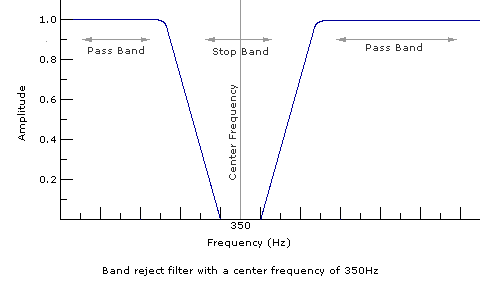
A band pass filter is like a low pass and a high pass filter used in combination to isolate a group of frequencies to pass through while everything else gets cut out. A band reject filter is the opposite of a band pass filter: a band of frequencies is blocked while everything else is let through.
Properties of filters
These filters have a number of attributes over which we have some control. For low pass and high pass filters, we can change the cutoff frequency, allowing control of the range of frequencies affected. Running a lead synthesizer through a low pass filter and slowly moving the cutoff frequency from high to low and back is a popular technique used in electronic dance music.
With band pass and band reject filters, rather than changing the cutoff frequency, we change the center frequency and width of the affected band.
With some filters we can also change the slope, which determines how quickly the stop band frequencies are reduced in level.
Many filters allow for a change in resonance or Q. Resonance occurs when sound in the pass band near the cutoff frequency is sent back into the filter as it comes out, creating feedback. The amount of feedback affects the volume of these frequencies, as well as the timbre of the sound. A wah-wah effect box is a resonant low pass filter with a foot pedal controlling the cutoff frequency.
Audio example of a low pass filter with resonance.
Let's add a low pass filter module to our imaginary synthesizer. We'll place it between the oscillator and our VCA. Depending on how we control it, this filter can make all kinds of changes to our synth sound, from gently decreasing the harshness of the high frequencies to making a variety of more intense special effects.
Here's a sample of what the synthesizer described in this diagram might sound like. As the sample progresses, the frequency of the low pass filter moves up and down again.
Here's a realization of this patch in PureData.
Control signals
In order to get the most mileage out of our synthesizer, we need a way of controlling each of its components internally. While many synthesizers have myriad knobs and buttons for controlling the sound, most people only have two hands, and it's difficult to accurately twist more than one or two knobs at a time. Fortunately, almost every module in a synthesizer can be controlled by another module. Our imaginary synthesizer does this already: the frequency of the oscillator and the volume level of the VCA are controlled by our keyboard.
Envelope generators
One way we can control signals within a synthesizer is by using a module called an envelope generator. When an envelope generator receives an "on" gate signal, it sends out a new signal that can be used to control another module. Unlike an oscillator, which repeats its signal over and over again, an envelope generator sends out its signal only once. Like an oscillator, we can look at the signal produced by an envelope generator on a time domain graph:
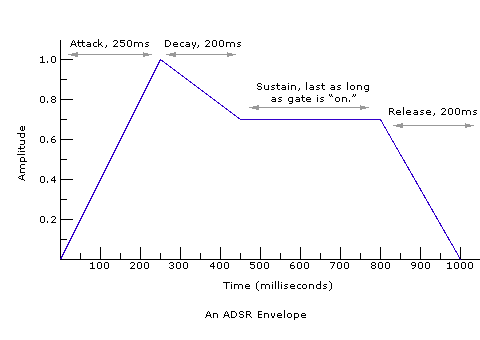
For every fraction a of a second the envelope generator is active, it sends a control signal that can be used to tell another module what to do. One way to think about envelopes is as maps for automatic knob control. For instance, the envelope pictured above starts by sending out a signal that gradually moves up from zero to one, which is like turning a knob from the far left, lowest position, to the far right, highest position. After that, the signal moves gradually down to about 0.7, which is like turning the knob to the left a little bit, and so on.
Envelopes like the one pictured here are called ADSR envelopes, so named for their four stages: Attack, Decay, Sustain, and Release. When we put an ADSR envelope module in a synthesizer, we specify exactly what is to happen during each stage of the envelope after an "on" gate signal is received. For example, the envelope pictured above has an attack stage that lasts 250 milliseconds, where the level increases to 1. After that, it has a decay stage lasting 200 milliseconds where the level decreases to 0.7. During the sustain stage, the level stays at 0.7 for as long as the envelope generator is receiving an "on" gate signal. Sustain stages do not have a specified duration. When the gate signal changes to "off," we enter the release stage, where the level takes 200 milliseconds to drop to 0.
ADSR envelopes are often used to control the volume of a sound, although they can be used to control almost anything inside a modular synthesizer. For example, the same envelope could control a resonant low pass filter, making a cool sweeping and wooshing effect evolve as we play each note.
Let's add an envelope generator to our synthesizer below. This envelope will cause the volume of the sound from the oscillator to fade in gradually, sustain, and then drop off sharply. We'll use an ADSR envelope generator connected to the level input of our VCA:

Here's a sample of what the synthesizer described in this diagram might sound like.
Here's a realization of this patch in PureData.
Low frequency oscillators (LFOs)
Another type of module frequently used to control other modules is the low frequency oscillator, or LFO. An LFO is just like a normal oscillator, it can have any waveform and amplitude we specify, but it has a very low, sub-audio frequency, producing a very slowly oscillating signal generally used to control other modules within a synthesizer. For example, an LFO might move the volume level of a VCA up and down, creating a tremolo effect. LFOs are like little robots that turn knobs back and forth for you.
Let's add an LFO to our synthesizer that causes the pitch of our oscillator to wiggle up and down a little bit, like a violinist moves their hand to create vibrato. We're also going to use the envelope generator to modulate the frequency of our filter, so we get a cool sweeping effect automatically on every note, especially if we turn up the filter's resonance. Using a control signal to change the frequency of another module is called frequency modulation, or FM, as indicated in the diagram below:

Here's a sample of what the synthesizer described in this diagram might sound like.
Here's a realization of this patch in PureData.
Conclusion and Further Reading
Almost every commercially available synthesizer and music synthesis software package operates using these basic principles. With this knowledge and some ingenuity, you'll never have to use a horrible synth preset again.
This is, however, not the end. There's quite a bit of excellent literature on sound synthesis and electronic music, and one of the best ways to learn is to read constantly. That said, here's some good stuff:
- The Computer Music Tutorial, by Curtis Roads
- The Csound Book, ed. Dr. Richard Boulanger
- Computer Music: Synthesis, Composition, and Performance, by Charles Dodge and Thomas Jerse
- Microsound, by Curtis Roads
- The Computer Music Journal
- Advanced Programming Techniques for Modular Synthesizers, ed. James J. Clark